3 Wprowadzenie do wnioskowania statystycznego

Chcemy się dowiedzieć czegoś na temat populacji (całości) na podstawie próby (części tej całości).

Przykładowo chcemy ocenić ile wynosi średnia waga główki kapusty na 100 h polu. Można ściąć wszystkie i zważyć, ale można też ściąć trochę (pobrać próbę się mówi uczenie) zważyć i poznać średnią na całym polu z dobrą dokładnością.

3.1 Masa ciała uczestników PŚ w rugby

W turnieju o Puchar Świata w rugby w 2015 roku uczestniczyło 623 rugbystów. Znamy szczegółowe dane odnośnie wzrostu i wagi każdego uczestnika turnieju. Obliczamy (prawdziwą) średnią, odchylenie standardowe i współczynnik zmienności masy ciała:

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    65,0    93,0   103,0   102,8   113,0   145,0

Czyli średnio rugbysta na turnieju ważył 102,8 kg (Mean na wydruku powyżej) a odchylenie standardowe (s) wyniosło 12,92 kg.

Rozkład, pokazany na rysunku 3.1, jest dwumodalny, bo w rugby są dwie grupy zawodników i wcale nie wszyscy ważą ponad 110 kilogramów.

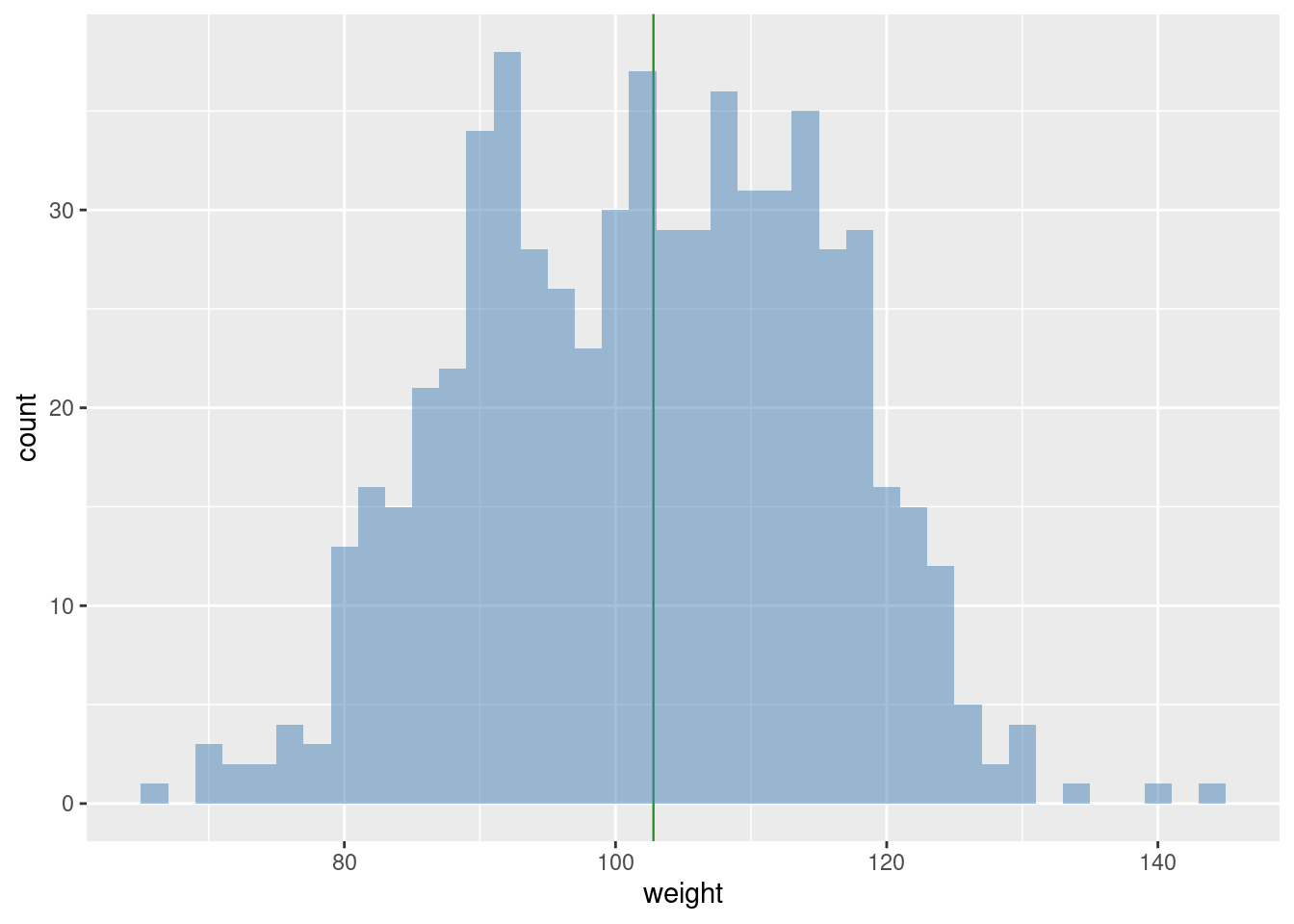
Rysunek 3.1: Rozkład wagi zawodników

Szacujemy średnią na podstawie 2 zawodników pobranych losowo.

Powtarzamy eksperyment 1000 razy (dwóch bo dla jednego nie obliczymy wariancji).

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    77,5    97,0   103,0   102,5   108,5   131,0

Średnia (średnich z próby) ma wartość 102,52 kilogramów a odchylenie standardowe 8,84 kilogramów. Wartość \(s/\sqrt{2}\) (odchylenie standardowe podzielone przez pierwiastek kwadratowy z liczebności próby) jest równa 9,14. Zauważmy, że ta wartość jest zbliżona do wartości odchylenia standardowego uzyskanego w eksperymencie (8,84 vs 9,14).

Zauważmy też, że wartość najniższej średniej wyniosła 77,5 kilogramów zaś najwyższej 131 kilogramów. Gdybyśmy mieli pecha i wylosowali te skrajnie nieprawdziwe wartości to mylimy się o 25,02 kilogramów na minus lub 28,48 kilogramów na plus.

Szacujemy średnią na podstawie 10 zawodników pobranych losowo.

Powtarzamy eksperyment 1000 razy.

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   91,22  100,10  103,10  102,99  105,70  116,90

Średnia ma wartość 102,99 kilogramów, a odchylenie standardowe 4,16 kilogramów. Wartość \(s/\sqrt{10}\) jest równa 4,09.

Szacujemy średnią na podstawie 40 zawodników pobranych losowo.

Uwaga: 40 zawodników to 6,4% całości. Powtarzamy eksperyment 1000 razy.

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   96,33  101,27  102,81  102,78  104,28  108,85

Średnia jest równa 102,78 kilogramów, a odchylenie standardowe 2,11 kilogramów. Wartość \(s/\sqrt{40}\) jest równa 2,04.

Zauważmy też, że wartość najniższej średniej wyniosła 96,325 kilogramów zaś najwyższej 108,85 kilogramów. Gdybyśmy mieli pecha i wylosowali te skrajnie nieprawdziwe wartości to mylimy się o 6,46 kilogramów na minus lub 6,07 kilogramów na plus. Niewątpliwie wynik znacznie lepszy niż dla próby dwuelementowej.

Podsumujmy eksperyment wykresem rozkładu wartości średnich (por. rysunek 3.2).

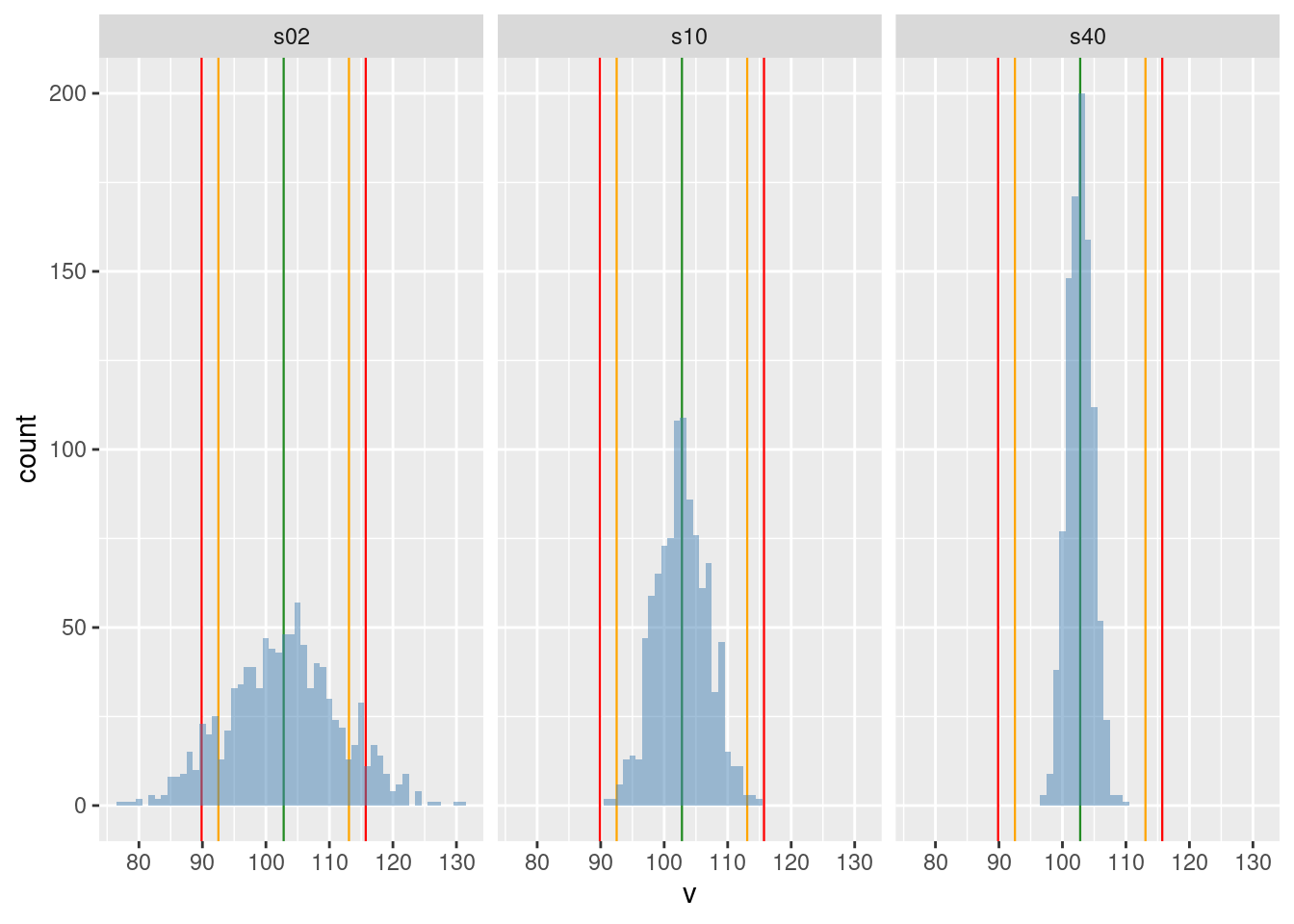
Rysunek 3.2: Rozkład średniej wagi rugbystów w zależności od wielkości próby

Wnioski z eksperymentu:

Wartość średnią wyznaczamy na podstawie jakiejś konkretnej metody. Wydaje się na podstawie powyższych eksperymentów, że z dobrym skutkiem możemy jako metodę wykorzystać średnią-z-próby.

W ogólności taką metodą, która formalnie jest funkcją elementów z próby, nazywa się w statystyce estymatorem. Warto to pojęcie zapamiętać. Wnioskujemy o wartości nieznanego parametru w populacji posługując się estymatorem.

Kontynuując wnioski z eksperymentu należy zauważyć, że wszystkie średnie-ze-średnich (bez względu na liczebność próby) są zbliżone do wartości prawdziwej (to się nazywa nieobciążoność estymatora); Mówiąc innymi słowy jeżeli będziemy oceniać wartość prawdziwej średniej na podstawie próby, a naszą ocenę powtórzymy wielokrotnie, to średnia będzie zbliżona do wartości prawdziwej (a nie np. niższa czy wyższa) Ta cecha jest niezależna od wielkości próby.

Jeżeli rośnie liczebność próby to zmienność wartości średniej-w-próbie maleje, co za tym idzie prawdopodobieństwo, że wartość oceniona na podstawie średniej z próby będzie zbliżona do wartości szacowanego parametru rośnie (to się nazywa zgodność). Co więcej, dobrym przybliżeniem zmienności średniej-w-próbie jest prosta formuła \(s/\sqrt{n}\) gdzie \(n\) jest liczebnością próby a \(s\) jest odchyleniem standardowym w populacji z której pobrano próbę.

Jeżeli mamy dwa różne estymatory służące do oszacowania parametru i oba są nieobciążone oraz zgodne, to który wybrać? Ten która ma mniejszą wariancję. Taki estymator nazywa się efektywny.

Estymator zatem powinien być nieobciążony, zgodny oraz efektywny (czyli mieć małą wariancję). Można matematycznie udowodnić, że pewien estymator ma tak małą wariancję, że niemożliwe jest wynalezienie czegoś jeszcze bardziej efektywnego. Takim estymatorem średniej w populacji jest średnia z próby.

Konkretną wartość estymatora dla konkretnych wartości próby nazywamy oceną (parametru).

3.2 Wiek kandydatów na radnych

W wyborach samorządowych w Polsce w roku 2018 o mandat radnego sejmików wojewódzkich ubiegało się 7076 kandydatów. Znamy szczegółowe dane odnośnie wieku każdego kandydata, bo to zostało publicznie podane przez Państwową Komisję Wyborczą. Obliczamy (prawdziwą) średnią, odchylenie standardowe i współczynnik zmienności wieku kandydatów:

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   18,00   34,00   46,00   46,24   58,00   91,00

Czyli średnio kandydat miał 46,24 lat a odchylenie standardowe wieku wyniosło 14,61 lat.

Rozkład znowu jest dwumodalny z jakiś powodów (por. rysunek 3.3).

Rysunek 3.3: Rozkład wieku kandydatów na radnych

Szacujemy średnią na podstawie 2 kandydatów pobranych losowo.

Powtarzamy eksperyment 1000 razy.

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   19,50   38,50   46,00   45,91   53,50   75,00

Średnia średnich z próby ma wartość 45,91 lat. Odchylenie standardowe wyniosło 10,71. Wartość \(s/\sqrt{2}\) jest równa 10,33.

Wartość najniższej średniej wyniosła 19,5 lat zaś najwyższej 75 lat. Gdybyśmy mieli pecha i wylosowali te skrajnie nieprawdziwe wartości to mylimy się o 26,41 lat na minus lub 29,09 lat na plus.

Szacujemy średnią na podstawie 10 kandydatów pobranych losowo.

Powtarzamy eksperyment 1000 razy.

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    32,5    43,1    46,3    46,3    49,3    60,6

Średnia średnich z próby ma wartość 46,3 lat. Odchylenie standardowe wyniosło 4,62. Wartość \(s/\sqrt{10}\) jest równa 4,62.

Szacujemy średnią na podstawie 40 kandydatów pobranych losowo

Uwaga: 40 kandydatów to ok. 0,6% całości. Powtarzamy eksperyment 1000 razy.

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   37,92   44,62   46,15   46,15   47,64   53,92

Średnia średnich z próby ma wartość 46,15 lat. Odchylenie standardowe wyniosło 2,3. Wartość \(s/\sqrt{40}\) jest równa 2,31.

Szacujemy średnią na podstawie 70 kandydatów pobranych losowo.

Uwaga: 70 kandydatów to około ok 1% całości (1000 powtórzeń).

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   40,94   45,03   46,29   46,29   47,52   51,71

Średnia średnich z próby ma wartość 46,29 lat. Odchylenie standardowe wyniosło 1,8 Wartość \(s/\sqrt{70}\) jest równa 1,75.

Wartość najniższej średniej wyniosła 40,94 lat zaś najwyższej 51,71 lat. Gdybyśmy mieli pecha i wylosowali te skrajnie nieprawdziwe wartości to mylimy się już tylko o 5,35 lat na minus lub 5,43 lat na plus.

Podsumujmy eksperyment wykresem rozkładu wartości średnich (rysunek 3.4).

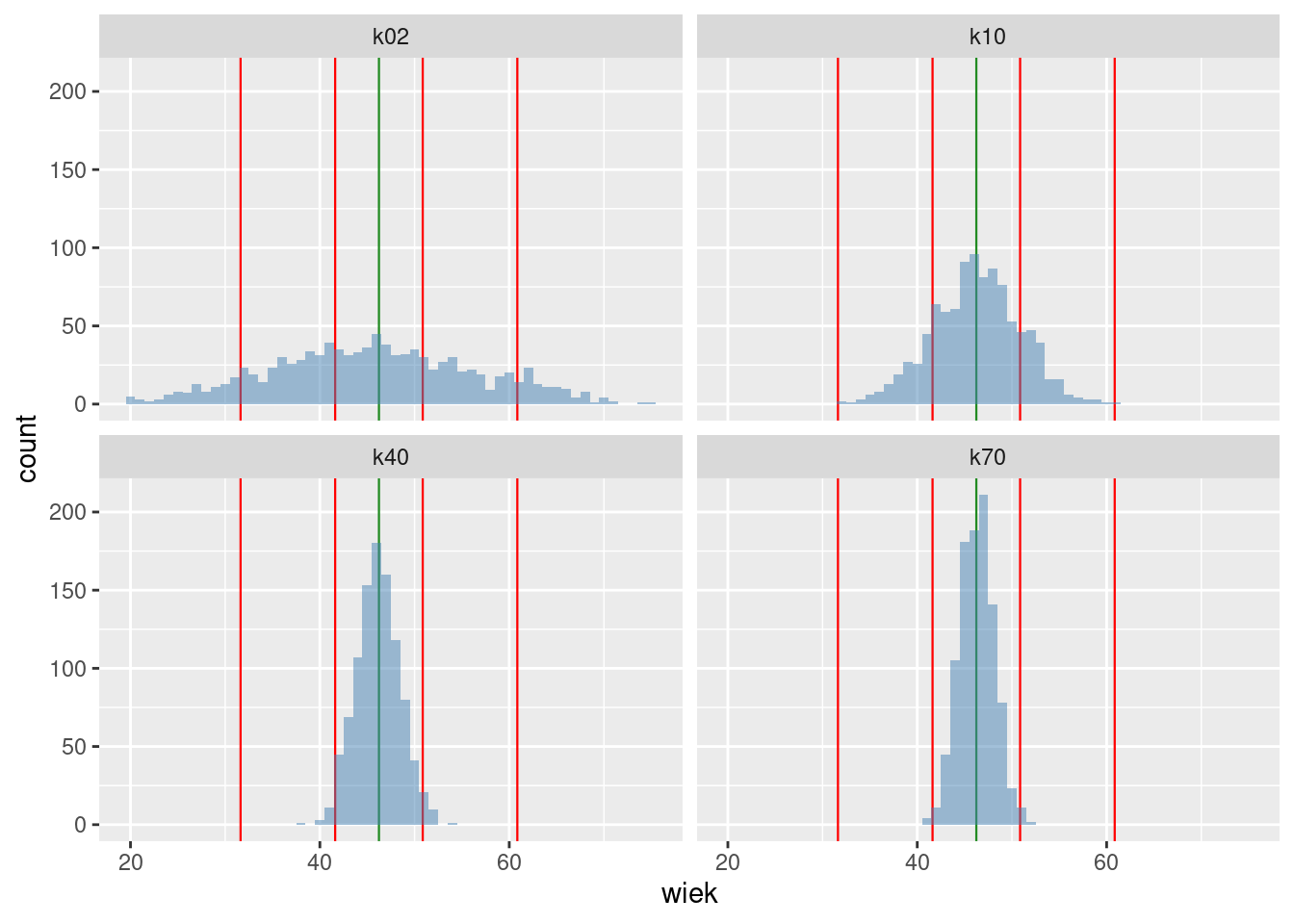
Rysunek 3.4: Rozkład średniej wieku kandydatów w zależności od wielkości próby

Obserwujemy to samo zjawisko, co w przypadku wagi rugbystów: im większa próba, tym dokładniejsza wartość średniej wieku. Bez względu na wielkość próby przeciętnie otrzymujemy prawdziwą wartość średniej.

Wnioski:

Precyzja wnioskowania zwiększa się wraz z liczebnością próby;
Precyzja wnioskowania zwiększa się tym szybciej im rozproszenie w populacji generalnej jest mniejsze;
Żeby z dużą dokładnością wnioskować o średniej dla dużej populacji wcale nie trzeba pobierać dużej próby (w ostatnim przykładzie było to 1% całości).

3.3 Rozkład normalny

Rozkład empiryczny zmiennej to przyporządkowanie kolejnym wartościom zmiennej odpowiadających im liczebności.

Załóżmy, że istnieje zapotrzebowanie społeczne na wiedzę na temat wieku kandydatów na radnych. Możemy to jak widać łatwo liczyć, ale jednocześnie jest to kłopotliwe. Należy do tego mieć zbiór ponad 7 tys liczb. Rozkład teoretyczny to matematyczne uogólnienie rozkładu empirycznego. Jest to model matematyczny operujący pojęciem (ściśle sformalizowanym) prawdopodobieństwa (zamiast liczebności). Rozkład teoretyczny jest:

zbliżony do empirycznego jeżeli chodzi o wyniki (jest przybliżeniem empirycznego);
jest zdefiniowany za pomocą kilku liczb; nie ma potrzeby korzystania z liczebności.

Okazuje się, że istnieje jeden rozkład teoretyczny, który z dobrą dokładnością opisuje rozkłady empiryczne będące wynikiem powyższej zabawy. Ten rozkład (zwany normalnym) zależy tylko od dwóch parametrów: średniej i odchylenia standardowego, gdzie średnia będzie równa (prawdziwej) średniej w populacji a odchylenie standardowe równe odchyleniu standardowemu w populacji podzielonemu przez pierwiastek z wielkości próby.

Przybliżenie za pomocą rozkładu normalnego średniego rozkładu wieku kandydatów na radnych dla próby 40- oraz 70-elementowej pokazuje rysunek 3.5.

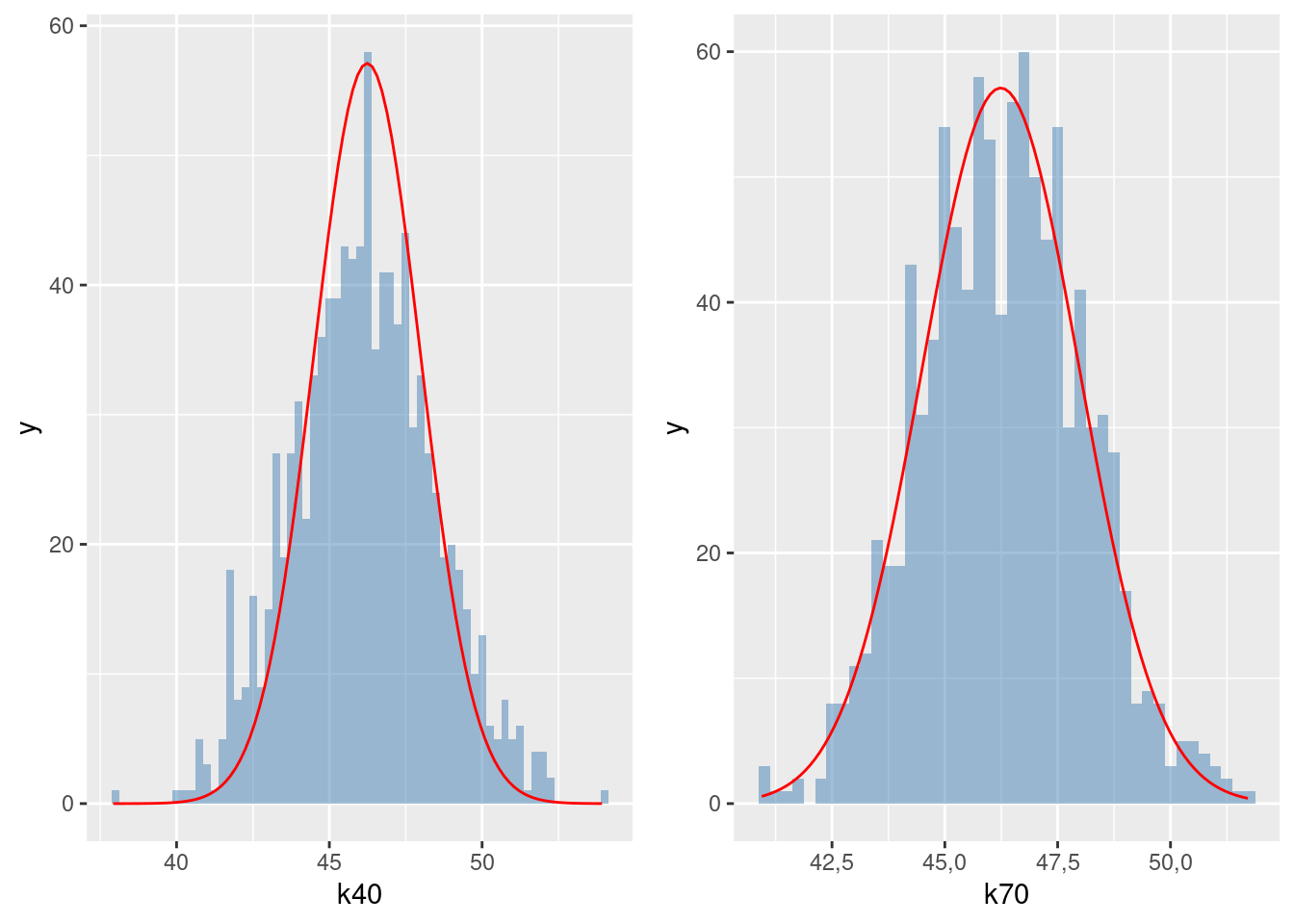
Rysunek 3.5: Rozkład normalny

Prawda, że wynik jest całkiem dobry? Teoretyczność czerwonej (w kolorowej wersji podręcznika) krzywej polega na tym, że ona zawsze będzie identyczna, podczas gdy histogram będzie różny. Gdybyśmy powtórzyli nasz eksperyment (generowania 1000 losowych prób przypominam), to zapewne trochę by się różnił, bo byśmy wylosowali inne wartości do prób. Ta teoretyczna abstrakcja określana jest prawdopodobieństwem. Rzucając monetą 1000 razy spodziewamy się po 500 orłów i reszek, co w modelu matematycznym będzie opisane jako: prawdopodobieństwo wyrzucenia orła wynosi 0,5. Rzucanie monetą to bardzo prosty eksperyment; nasz z liczeniem średniej wieku jest bardziej skomplikowany więc miło jest się dowiedzieć, że używając czerwonej krzywej można łatwo obliczyć jak bardzo prawdopodobne jest na przykład popełnienie błędu większego niż 10% średniej, albo większego niż 0,1 lat. Albo jak duża powinna być próba żeby ten błąd był nie większy niż 0,1 lat.

Interpretacja wartości rozkładu empirycznego zwykle jest w kategoriach ryzyka/szansy czy prawdopodobieństwa. Przykładowo interesuje nas prawdopodobieństwo, że kandydat ma mniej niż 30 lat. Takich kandydatów jest 1091 a wszystkich kandydatów dla przypomnienia jest 7076. Iloraz tych wartości będzie interpretowany jako ryzyko/szansa/prawdopodobieństwo (wynosi ono 15,42%).

Podobnie można obliczyć prawdopodobieństwo, że wiek kandydata będzie się zawierał w przedziale 50–60 lat. Ponieważ kandydatów w wieku 50–60 lat jest 1570, to szukane prawdopodobieństwo jest równe: 22,19%).

Jeżeli zamiast rozkładu empirycznego będziemy używać rozkład normalnego, który jak widzimy jest jego dobrym przybliżeniem, to nie musimy liczyć empirycznych liczebności. Wystarczy, że znamy średnią i odchylenie standardowe a potrafimy obliczyć każde prawdopodobieństwo dla każdego przedziału wartości zmiennej.

W szczególności dla rozkładu normalnego prawdopodobieństwo przyjęcia wartości z przedziału \(m \pm s\) (średnia plus/minus odchylenie standardowe) wynosi około 0,68 prawdopodobieństwo przyjęcia wartości z przedziału \(m \pm 2 \times s\) wynosi około 0,95 a przyjęcia wartości z przedziału \(m \pm 3 \times s\) około 0,997. Czyli w przedziale \([-3s < m, m +3s]\) znajdują się praktycznie wszystkie wartości rozkładu. Albo innymi słowy przyjęcie wartości spoza przedziału średnia plus/minus trzykrotność odchylenia standardowego jest bardzo mało prawdopodobna.

Za pomocą rozkładu normalnego można opisać rozkład wagi rugbystów, wieku posłów, wagę noworodków i miliony innych rozkładów. Uogólnieniem teoretycznym pojęcia zmiennej statystycznej, które do tej pory używaliśmy jest zmienna losowa, tj. zmienna, która przyjmuje wartości liczbowe z określonym prawdopodobieństwem np. określonym przez rozkład normalny.

3.4 Odsetek kobiet wśród kandydatów na radnych

Dane dotyczące kandydatów na radnych do sejmików wojewódzkich zawierają także płeć kandydata. Ktoś może być ciekaw jaki był odsetek kobiet w tej grupie. Taki parametr nazywa się proporcją albo ryzykiem, a potocznie i niefachowo procentem. Matematycznym modelem jest zmienna dwuwartościowa, która z określonym prawdopodobieństwem przyjmuje wartość kobieta. Obliczmy empiryczną wartość tego prawdopodobieństwa jako liczbę kobiet do liczby wszystkich kandydatów. Wartość tego parametru wynosi 0,4587 (albo 45,87%). Potraktujmy to jako prawdziwą wartość prawdopodobieństwa (p), że kandydat jest kobietą i empirycznie sprawdźmy czy możemy szacować o prawdziwej wartości tego parametru używając (jako estymatora żeby się przyzwyczajać do nowych terminów) proporcji z próby. Tradycyjnie powtarzamy eksperyment 1000 razy dla trzech różnych wielkości próby. Rozkład otrzymanych wartości przedstawia rysunek 3.6.

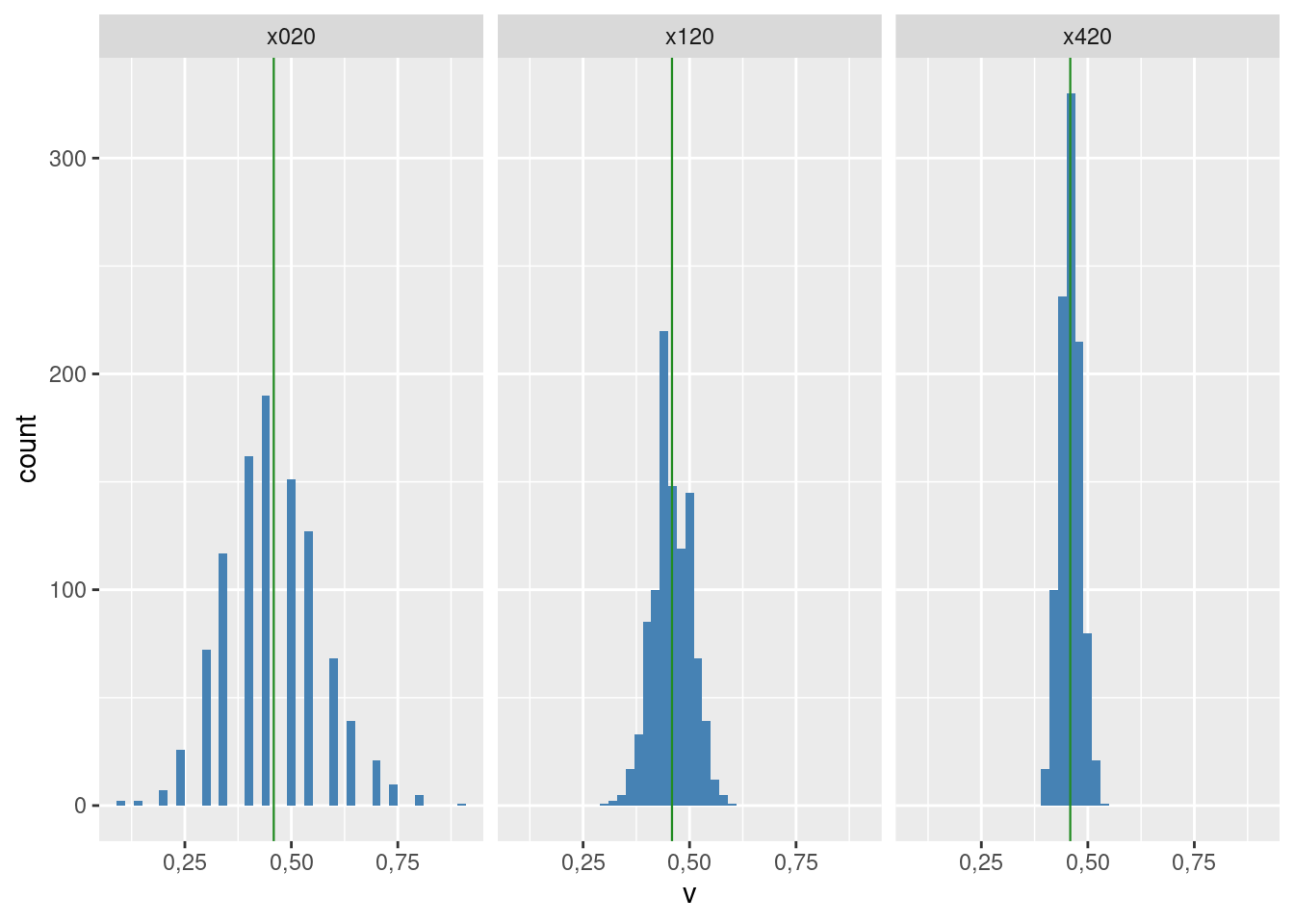
Rysunek 3.6: Rozkład wielkości p dla różnej wielkości próby

Wnioski:

Dla próby 20 elementowej rozkład nie przypomina rozkładu normalnego.
Dla prób 120 i 420 elementowej rozkład jest podobny do normalnego.
Zmienność estymatora maleje wraz ze wzrostem liczebności próby; każe nam to przypuszczać (i tak jest w istocie) że jest on zgodny.
W każdym przypadku średnia z 1000 eksperymentów jest zbliżona do wartości prawdziwej; każe nam to przypuszczać (i tak jest w istocie) że estymator jest nieobciążony.

Rozkład normalny jest tak magiczny że nawet jeżeli zmienna, której parametr szacujemy nie ma rozkładu zbliżonego do normalnego (jak w przypadku zmiennej, która przyjmuje tylko dwie wartości) to i tak estymator tego parametru będzie normalny. Co najwyżej będziemy potrzebowali większej próby żeby „znormalniał” (jak w opisywanym przykładzie).

3.5 Wnioskowanie statystyczne

Celem analizy danych z próby jest uogólnienie uzyskanych wyników na całą populację. To uogólnienie nazywa się wnioskowaniem (interferance). Przypominamy, że wnioskujemy o wartości parametru w populacji posługując się estymatorem. W przypadku wnioskowania o średniej estymatorem jest średnia-z-próby. Dobrze by było wiedzieć jak bardzo wiarygodna jest ta wartość (zwana oceną parametru) uzyskana na podstawie konkretnego estymatora, inaczej mówiąc jak dużo mogliśmy się pomylić.

Do oceny tej wiarygodności można użyć wariancji-średniej-z-próby, która nazywa się wariancją błędu (error variance). Jeżeli wariancja błędu jest duża, to średnia obliczona na podstawie próby może znacznie się różnić od prawdziwej średniej. Jeżeli wariancja błędu jest mała, to wartości bardzo różniące się od prawdziwej średniej mają małe szanse na zaistnienie. W przypadku rozkładu normalnego wiemy, że wariancja błędu jest równa \(s^2/n\) (gdzie \(s^2\) jest wariancją w populacji, a \(n\) wielkością próby).

W ramach wnioskowania stosowane są trzy metody (podejścia):

estymacja punktowa,
estymacja przedziałowa,
testowanie hipotez.

3.5.1 Estymacja punktowa

Szacujemy średnią (albo inny parametr) i tę wartość uznajemy za wartość prawdziwą; dokładność szacunku jest nieokreślona. Inaczej mówiąc wartość estymatora dla konkretnej próby przyjmujemy za ocenę parametru.

Estymatorem punktowym średniej jest średnia z próby a estymatorem punktowym proporcji/ryzyka jest proporcja/ryzyko z próby.

3.5.2 Estymacja przedziałowa

Nie można ustalić prawdopodobieństwa popełnienia błędu dla dokładnej wartości parametru (co wynika z właściwości matematycznych modelu), ale można dla dowolnego przedziału od–do.

Czyli nie można ustalić, że z prawdopodobieństwem 95% oszacujemy wartość średnią czegoś jako 5,000000, ale można z prawdopodobieństwem 95% oszacować przedział, w którym znajdzie się średnia (przykładowo, że będzie to przedział 4,9–5,1).

Estymacja przedziałowa to oszacowanie przedziału wartości od–do, który z zadanym z góry prawdopodobieństwem zawiera prawdziwą wartość parametru.

Z góry wyznaczone prawdopodobieństwo nazywa się poziomem ufności (określa jak często mamy się NIE pomylić).

3.5.3 Testowanie hipotez

Większość analiz statystycznych polega na porównaniu. W wyniku tego porównania otrzymujemy liczbę. Załóżmy, że mamy dwie próby dotyczące wieku kandydatów na radnych do sejmików wojewódzkich z roku 2018 (średnia 46,1) oraz z roku 2014 (47,2). Różnica wynosi 1,1 lat i może być spowodowana błędem przypadkowym (tj. gdybyśmy wylosowali jeszcze raz dwie próby, to wynik byłby zupełnie odmienny np 46,9 vs 46,5) i/lub wynikać z tego, że faktycznie w roku 2014 kandydaci byli starsi.

Formalnie stawiamy hipotezę, że różnica średnich wynosi zero. Jest to tzw. hipoteza zerowa. Niezbędne jest także postawienie hipotezy alternatywnej, którą może być proste zaprzeczenie zerowej. Zapisuje się to następująco (\(m_{14}\)/\(m_{18}\) oznacza odpowiednio średnie w latach 2014/2018):

\(H_0\): różnica średnich wieku wynosi zero (\(m_{14} = m_{18}\))

\(H_1\): różnica średnich wieku jest różna od zera (\(m_{14} \not= m_{18}\))

Hipotezy sprawdzamy wykorzystując test statystyczny czyli zmienną losową, której rozkład prawdopodobieństwa zależy (jest funkcją powiedziałby matematyk) od wartości testowanych parametrów (w tym przypadku \(m_{14}\) oraz \(m_{18}\)). Tę zmienną losową nazywa się statystyką testu.

Nie jest chyba wielkim zaskoczeniem, że statystyką testu w teście różnicy średnich jest różnica średnich w próbie (poprawnie mówiąc różnica uwzględniająca liczebność próby oraz zmienność obu populacji). Całkiem zdroworozsądkowo możemy przyjąć, że duże wartości statystyki testu świadczą na rzecz hipotezy alternatywnej, natomiast małe na rzecz hipotezy zerowej.

Duża różnica pomiędzy hipotezą a wynikiem z próby może wynikać z tego, że:

Pechowo trafiła nam się nietypowa próba, który zdarza się rzadko (rozkład normalny).
Hipoteza jest fałszywa, średnie mają inną wartość niż zakładamy w hipotezie zerowej.

Statystyk zawsze wybierze drugą wersję. Pozostaje tylko ustalić co to jest rzadko (dla statystyka)?

Rzadko, to z prawdopodobieństwem mniejszym niż z góry ustalone małe prawdopodobieństwo zwane poziomem istotności. Określa ono jak często możemy się pomylić odrzucając hipotezę zerową, która jest prawdziwa.

Teraz wystarczy obliczyć prawdopodobieństwo wystąpienia różnicy, którą otrzymaliśmy lub jeszcze większej i porównać je z poziomem istotności. Jeżeli to prawdopodobieństwo jest równe lub niższe od poziomu istotności odrzucamy hipotezę zerową (różnica jest istotna statystycznie).

Przyjmijmy przykładowo, że prawdopodobieństwo wystąpienia różnicy 1,1 lat (i większej) oszacowane na podstawie odpowiedniego modelu matematycznego (rozkład normalny) wynosi 0,3 co znaczy że coś takiego zdarza się względnie często – trzy razy na 10 pobranych prób.

Załóżmy z kolei że, ta różnica wyniosła 3,2 lata. Prawdopodobieństwo wystąpienia takiej różnicy (i większej) wynosi 0,009 co znaczy że coś takiego zdarza się względnie rzadko – 9 razy na tysiąc prób.

Przyjmując, że możemy się mylić 5 razy na 100 w pierwszym przypadku statystyk powie, że nie ma podstaw do odrzucenia hipotezy \(H_0\). Różnica 1,1 lat wynika z przypadku. W drugim wypadku statystyk powie, że hipoteza jest fałszywa, bo zdarzyło się coś co nie powinno się zdarzyć.

Ale jest jeszcze drugi przypadek popełnienia błędu: przyjmujemy hipotezę zerową, która jest fałszywa. W testach statystycznych nie określa się prawdopodobieństwa popełnienia tego błędu, a w związku z tym nie można przyjąć hipotezy zerowej (bo nie znamy ryzyka popełnienia błędu).

W konsekwencji hipotezę zerową albo się odrzuca albo nie ma podstaw do odrzucenia. Wniosek cokolwiek niekonkluzywny, ale tak jest.

Dlatego też często „opłaca się” tak postawić hipotezę zerową aby ją następnie odrzucić, bo taki rezultat jest bardziej konkretny.

3.5.4 Testy nieparametryczne

Można testować hipotezy na temat wartości parametrów, ale można też testować przypuszczenia o charakterze mniej konkretnym. Na przykład, że dwie zmienne są niezależne (co to znaczy wyjaśniono w następnym rozdziale), albo że dwa rozkłady są podobne do siebie (rozkłady nie średnie). Takie hipotezy/testy określa się jako nieparametryczne. Przykładami są testy niezależności chi-kwadrat albo normalności Shapiro-Wilka (opisane w następnym rozdziale).

Oczywiste, ale powtórzmy: przypuszczenia o charakterze nieparametrycznym możemy tylko testować (sprawdzać hipotezy); nie obliczamy wtedy ani ocen ani nie wyznaczamy przedziałów ufności.

3.6 Statystyk Carl Pearson

W punkcie 2.3 przypomnieliśmy postać Florence Nightingale – matki statystyki i bardzo dobrej kobiety. A kto był ojcem tejże statystyki? Ojców było więcej niż matek oczywiście, a wśród nich Francis Galton (regresja), Carl Pearson (współczynnik korelacji liniowej, test niezależności chi-kwadrat) oraz Ronald Fisher (podstawy wnioskowania). Niestety wszyscy wymienieni byli zadeklarowanymi rasistami oraz wyznawcami społecznego darwninizmu i eugeniki. Pierwszymi zastosowaniami „nowoczesnych” metod statystycznych było naukowe udowodnienie, że biali ludzie są lepsi od innych:

Przez ile stuleci, ile tysięcy lat Kaffirowie […] lub Murzyni rządzili w Afryce nie niepokojeni przez białych ludzi? Jednak ich walki międzyplemienne nie stworzyły cywilizacji w najmniejszym stopniu porównywalnej z aryjską […] Historia pokazuje jeden i tylko jeden sposób, w jaki powstaje wysoka cywilizacja, a mianowicie walka rasy i przetrwanie rasy sprawniejszej fizycznie i psychicznie…

Powyższe to cytat z National Life from the standpoint of science Carla Pearsona (Londyn 1905).

Naszym zdaniem dobrze jest pamiętać o tym fatalnym starcie „nowoczesnej statystyki”, bo chociaż jest mało prawdopodobne, że zostanie ona znowu wykorzystania do równie odrażających celów, to jest raczej więcej niż pewne, że będzie użyta do innych szwindli. Jeszcze jeden argument żeby nie traktować wyników analiz statystycznych jako wiedzy objawionej, absolutnie pewnej i 100% prawdziwej (por. uwagę w punkcie 1.1).

3.7 Słownik terminów, które warto znać

Estymacja (punktowa, przedziałowa): szacowanie wartości parametru na podstawie próby.
Estymator (nieobciążony, zgodny, efektywny): funkcja na wartościach próby która służy do oszacowania parametru.
Hipoteza statystyczna: przypuszczenie dotyczące parametru lub rozkładu zmiennej.
Ocena (parametru): konkretna wartość estymatora dla pewnej próby.
Poziom istotności (testu; oznaczany jako \(\alpha\); zwykle 0,05): prawdopodobieństwo popełnienia błędu.
Poziom ufności: prawdopodobieństwo, że przedział ufności zawiera prawdziwą wartość parametru; oznaczany jako \(1- \alpha\); zwykle 0,95.
Rozkład (prawdopodobieństwa): przypisanie prawdopodobieństwa wartościom zmiennej losowej.
Test statystyczny: metoda weryfikacji hipotezy statystycznej.
Wnioskowanie statystyczne: wnioskowanie o całości na podstawie próby.