6 Praca z programem Jamovi

Jak wspomniano w rozdziale 1, statystkę można uprawiać (tj. liczyć statystyki w drugim tego słowa znaczeniu), wykorzystując różne programy. My zdecydowaliśmy się promować Jamovi, program, który naszym zdaniem jest najlepszym – z punktu widzenia większości studentów nauk o zdrowiu – połączeniem ceny, możliwości, prostoty i łatwości nauki.

6.1 Podstawy pracy z Jamovi

Jamovi jest oprogramowaniem rozpowszechnianym na licencji typu Open Source, a więc można go używać za darmo. Program jest dostępny ze strony https://www.jamovi.org/download.html. Klikamy, ściągamy, uruchamiamy instalator. Program jest dość duży, ale to nie jest aż tak wielki problem w czasach kiedy pojemności dysków w domowym komputerze zaczynają się od 250 gigabajtów. Jest też wersja Jamovi365, którą można posługiwać się w przeglądarce i wtedy nie trzeba instalować niczego na swoim komputerze.

W podręczniku pokazujemy, jak uprawiać statystykę z tradycyjną wersją Jamovi. Po zainstalowaniu uruchamiamy program, którego ekran startowy wygląda jak na rysunku 6.1.

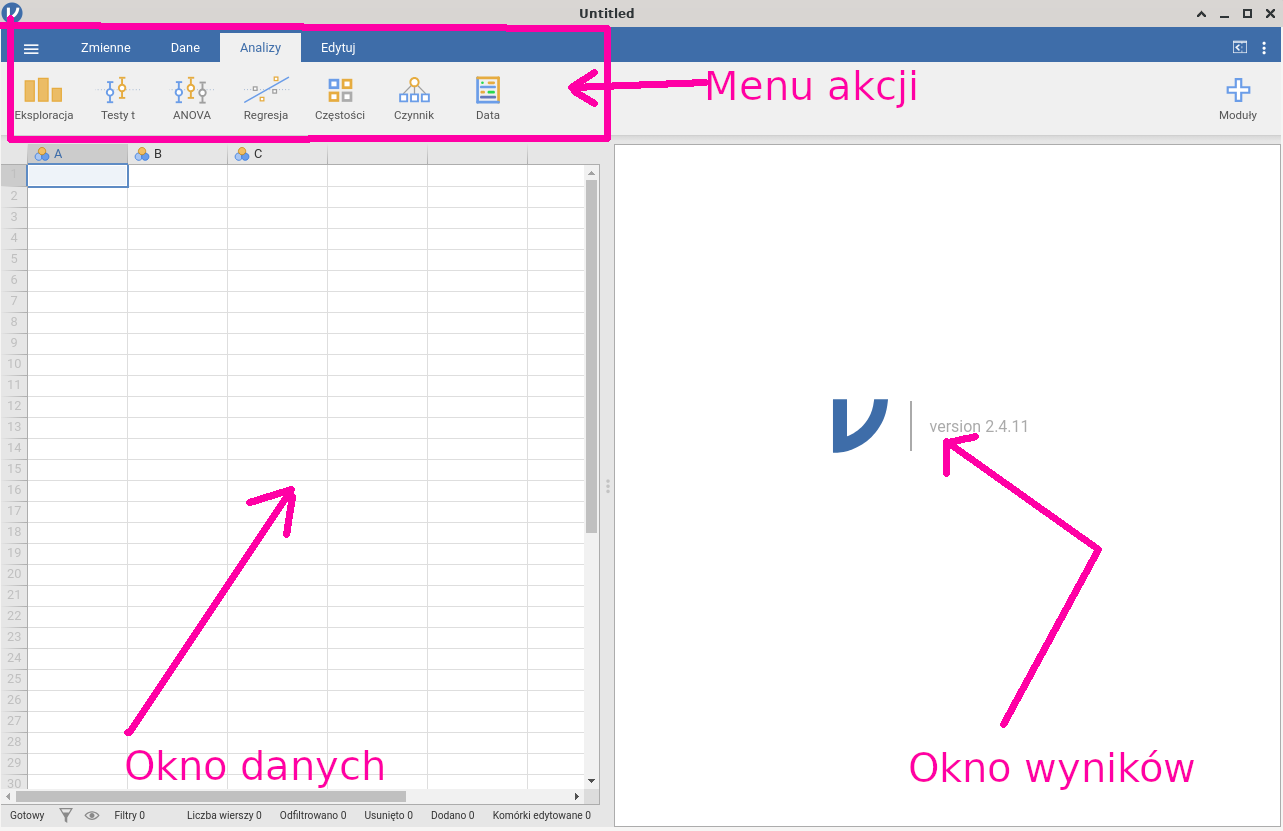
Rysunek 6.1: Ekran startowy Jamovi

Menu akcji umożliwia wykonanie podstawowych akcji:

wczytanie danych i zapisanie danych (pierwsza pozycja menu oznaczona jako trzy poziome kreski);
podgląd (w sensie skontrolowania wartości zmiennych) i modyfikację danych (pozycje Zmienne oraz Dane);
wykonanie obliczeń (pozycja Analizy);
modyfikowanie raportu (pozycja Edit).

Typowa sesja w Jamovi:

Wczytanie danych z pliku o praktycznie dowolnym formacie. Jeżeli przykładowo dane są wynikiem wykonania badania ankietowego z wykorzystaniem Formularzy Google’a to zalecamy posługiwanie się formatem CSV.
Transformacja danych. Przekodowanie wartości nominalnych na rangi. Przekodowanie wartości liczbowych na nominalne. Odwrócenie pytań odwróconych. Obliczenie sum/średnich rang dla wielu zmiennych.
Wykonanie obliczeń:
1. Analiza struktury (Eksploracja).
2. Analiza zależności między zmienną liczbową a nominalną (testy t/ANOVA).
3. Analiza zależności między zmiennymi liczbowymi: współczynnik korelacji liniowej/macierz korelacji (Regresja).
4. Analiza zależności między zmienną liczbową a zmiennymi liczbowymi/nominalnymi: regresja liniowa i logistyczna (Regresja).
5. Analiza zależności między zmiennymi nominalnymi: tablica wielodzielna, test chi-kwadrat (Częstości).
Wykonanie obliczeń jest banalnie proste i sprowadza się do wybrania myszką odpowiednich zmiennych oraz procedury, która ma być wykonana. Wynik obliczeń pojawia się natychmiast w oknie wyników. Jeżeli coś nam nie wyszło, można procedurę poprawić, a poprzedni wynik usunąć z okna wynikowego.
Zapisania danych (pozycja trzy poziome kreski). Po skończeniu pracy wynik można zapisać, żeby np. wysłać wykładowcy lub nie zaczynać od zera jeżeli będziemy musieli pracę kontynuować, bo wykładowca chciał, żebyśmy coś poprawili.

6.2 Analiza ankiety satysfakcja – wiedza o paleniu – zamiar odejścia

Przykład nieco absurdalny, ale za to w zwartej postaci ilustrujący praktyczne sposoby transformacji danych oraz wykorzystania wszystkich procedur omawianych w podręczniku.

6.2.1 Wczytanie danych

W wyniku przeprowadzenia badania ankietowego zebrano za pomocą Formularza Google’a dane dotyczące satysfakcji/zamiaru odejścia oraz wiedzy nt. szkodliwości palenia tytoniu. Wyniki wyeksportowano do arkusza kalkulacyjnego, którego początek wygląda jak na rysunku 6.2:

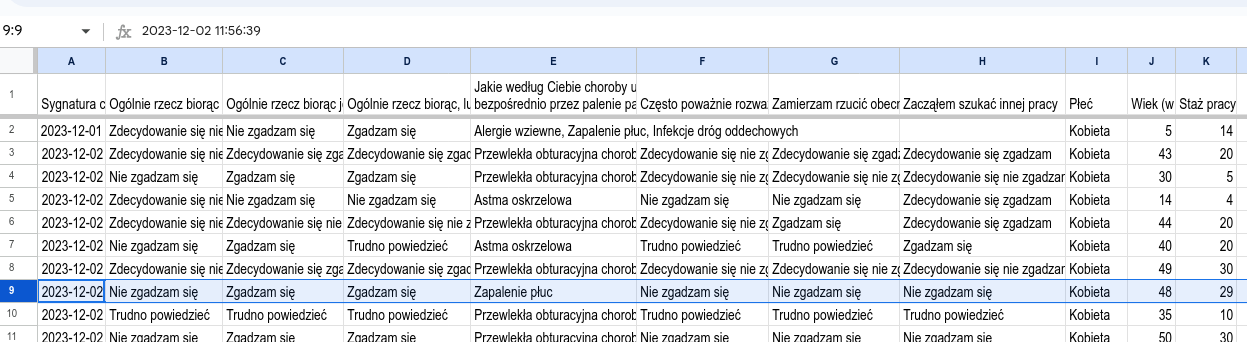
Rysunek 6.2: Fragment przykładowej ankiety

Ankieta składa się z 10 następujących pytań:

Ogólnie rzecz biorąc, nie lubię swojej pracy (kolumna B), Ogólnie rzecz biorąc, jestem zadowolony ze swojej pracy (C), Ogólnie rzecz biorąc, lubię tu pracować (D), Jakie według Ciebie choroby układu oddechowego mogą być spowodowane bezpośrednio przez palenie papierosów? (E), Często poważnie rozważam odejście z obecnej pracy (F), Zamierzam rzucić obecną pracę (G), Zacząłem szukać innej pracy (H), Płeć (I), Wiek (w latach) (J), oraz Staż pracy (K).

Ponadto Formularz Google’a dodał automatycznie sygnaturę czasową jako zawartość pierwszej kolumny (A).

Zmieniamy wartości w pierwszym wierszu, który powinien zawierać nazwy zmiennych. Nazwy zmiennych powinny być jednowyrazowe i w miarę krótkie, żeby się później można nimi wygodnie posługiwać. Jednocześnie nie powinny być za krótkie, żeby od razu było widać, jakie dane zawiera zmienna.

Jak widać, pytania z kolumn B–D mierzą to samo (satysfakcję), więc zmieniamy im nazwę na bardziej zwartą s1, s2 oraz s3 (s od satysfakcja). Podobnie ponieważ pytania z kolumn F–H też mierzą to samo (zamiar odejścia), to też zmieniamy nazwy na coś krótszego: zo1, zo2, zo3. Kolumnę E nazywamy wiedza_nt_palenia a kolumny I, J oraz K odpowiednio: plec, wiek oraz staz.

Teraz arkusz wygląda jak na rysunku 6.3.

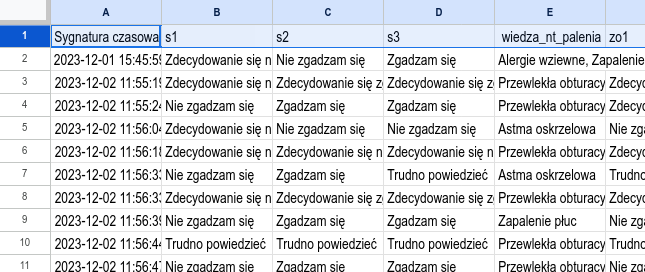
Rysunek 6.3: Fragment przykładowej ankiety

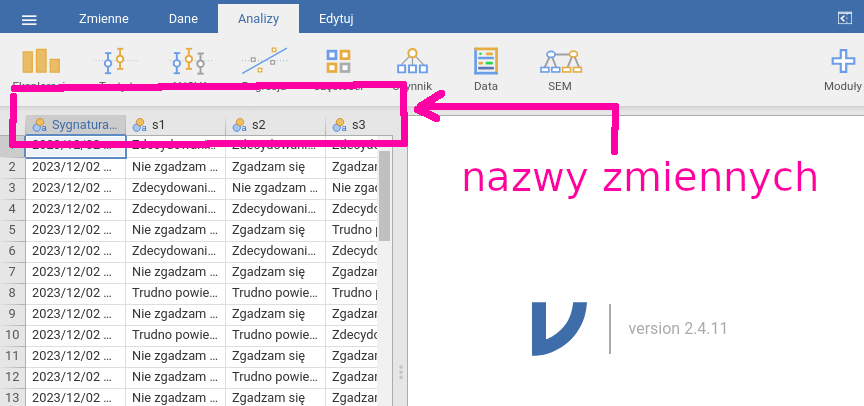
Arkusz eksportujemy, wybierając format CSV. Bez problemu powinniśmy go wczytać do Jamovi (trzy poziome kreski →Otwórz). Jeżeli import się powiódł, to powinniśmy zobaczyć coś podobnego do tego, co widać na rysunku 6.4.

Reasumując:

Pytania oznaczone jako s1/s2/s3 mierzą satysfakcję z pracy; pytania zo1/zo2/zo3 mierzą zamiar odejścia z pracy. Pytania s1–s3 oraz zo1–zo3 są pytaniami jednokrotnego wyboru.
Pytanie oznaczone jako wiedza_nt_palenia mierzy wiedzę na temat palenia tytoniu. Jest to przykład wykorzystania pytania z wielokrotnym wyborem.
Pytania plec, wiek, staz mierzą płeć (kobieta/mężczyzna), wiek (lata ukończone) oraz staż pracy (lata przepracowane).
Pierwsza kolumna nie jest potrzebna, ale jest dodawana przez aplikację Formularze Google.

Rysunek 6.4: Import danych

6.2.2 Przekodowanie danych

Zwykle zawartość arkusza zawierającego wyniki ankiety wymaga przekodowania. W naszym przykładzie należy wykonać:

Zmienne s1–s3 oraz zo1–zo3 są mierzone w skali porządkowej. Wartości tych zmiennych chcemy zmienić (przekodować) na rangi według schematu: Zdecydowanie się nie zgadzam = 1; Nie zgadzam się = 2; Trudno powiedzieć = 3 itd. Dodatkowo zauważmy, że s1 jest pytaniem odwróconym. W takich pytaniach należy przeliczyć rangi według prostej formuły s1r = 6 - s1.
- Miarą satysfakcji będzie suma rang s1r+s2+s3.
- Miarą zamiaru odejścia będzie suma rang zo1+zo2+zo3.
Zmienna plec jest mierzona w skali nominalnej. Nie musimy jest przekodowywać.
Wartość zmiennej wiedza_nt_palenia należy przekodować na liczbę według schematu: za wybranie poprawnej odpowiedzi plus jeden punkt; za wybranie błędnej odpowiedzi minus jeden punkt.
- Miarą wiedzy nt. palenia będzie suma punktów uzyskanych za odpowiedzi prawidłowe minus suma punktów uzyskanych za odpowiedzi nieprawidłowe.

Uwaga: Sposób mierzenia wiedzy nt. palenia jest niepotrzebnie skomplikowany; zamiast pytania z wielokrotnym wyborem spośród 8 możliwości/wariantów prościej jest zastosować 8 pytań Tak/Nie, po czym pytania poprawne zsumować, pytania niepoprawne też dodać, a wartość odjąć od sumy uzyskanej dla pytań poprawnych. My o tym wiemy, że tak jest bez sensu, ale pokazujemy jako przykład przekodowania pytania z wielokrotnym wyborem.

Wartości zmiennych wiek oraz staz są liczbami. Mogą być analizowane tak-jak-są (regresja/korelacja), ale można też je przekodować na wartości nominalne (mały-średni-duży staż) i zastosować metody z grupy zmienna–liczbowa/zmienna nominalna (takie jak test ANOVA czy Kruskala-Wallisa).

Przekodowanie wykonujemy, wybierając Dane w menu głównym.

Klikamy w nazwę zmiennej, którą zamierzamy przekodować. Niech to będzie s1. Kolumna po kliknięciu zmieni kolor.
Wybieramy ikonę Przekształcenie. Wypełniamy jak na rysunku 6.5.

Uwaga: Jamovi nie zmieni wartości zmiennej s1, tylko utworzy nową zmienną z przekodowanymi wartościami. Zmienna, na podstawie której jest tworzona nowa zmienna, nazywa się źródłową (s1 w naszym przykładzie jest źródłowa).

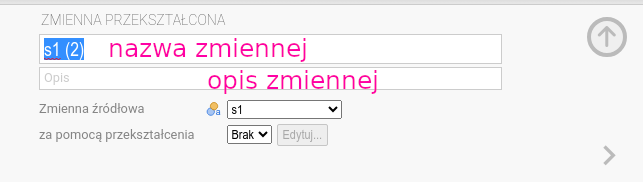
Rysunek 6.5: Przekształcenie

Wpisujemy sensowną nazwę (np. s1p od przekodowana). Jeśli będziemy używać sensownych nazw, łatwiej będzie nam się pracowało. Dobrze jest też podać w opisie, co zawiera zmienna.

Klikamy w pole wyboru na dole (obok napisu za pomocą przekształcenia). Powinniśmy zobaczyć coś podobnego do tego, co widać na rysunku 6.6.

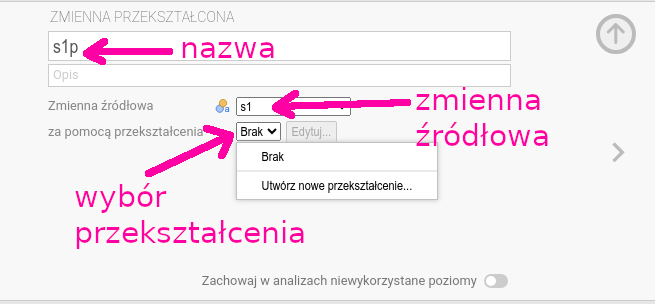
Rysunek 6.6: Przekształcenie

Wybieramy Utwórz nowe przekształcenie. Wpisujemy sensowną nazwę przekształcenia (np. Likert2R5) oraz formułę przekształcenia:

IF ($source=="Zdecydowanie się nie zgadzam", 1,
 IF ($source=="Nie zgadzam się", 2,
   IF ($source=="Trudno powiedzieć", 3,
      IF ($source=="Zgadzam się", 4, 5))))

Formuła może wydawać się przerażająca, ale jest koncepcyjnie bardzo prosta:

IF (warunek, jeżeli-prawda, jeżeli-fałsz)

Warunek to fragment $source=="Zdecydowanie się nie zgadzam":

$source oznacza bieżącą wartość zmiennej źródłowej;
== to operator równości; jest więcej operatorów, które można wybrać z menu;
$source=="Zdecydowanie się nie zgadzam" oznacza, że jeżeli bieżącą wartością w kolumnie źródłowej jest Zdecydowanie się nie zgadzam to wykonaj jeżeli-prawda; w wypadku przeciwnym wykonaj jeżeli-fałsz.

Część jeżeli-prawda to zwykle wstawienie nowej wartości; jeżeli-fałsz to często następna formuła IF albo wstawienie innej nowej wartości. Przykładowo jeżeli bieżącą wartością w kolumnie źródłowej jest Zdecydowanie się nie zgadzam, to wstaw 1, jeżeli nie – to wstaw 0:

  IF ($source=="Zdecydowanie się nie zgadzam", 1,0)

Ponieważ w przykładzie mamy do przekodowania nie dwie, a pięć wartości, musimy użyć czterech warunków, które są zagnieżdżone jeden w drugim (por. rys. 6.7).

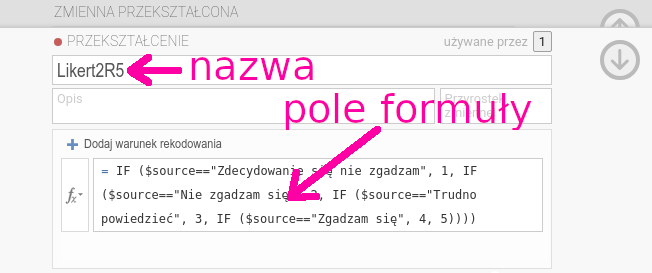
Rysunek 6.7: Przekształcenie

Naciskamy Enter i gotowe. Zostaje utworzona zmienna s1p zawierająca zamiast napisów rangi.

Jeżeli uporaliśmy się z przekodowaniem s1, ustawiamy kursor na s2 w oknie danych. Naciskamy ikonę Przekształcenie. Upewniamy się, że zmienną źródłową jest s2. Zmieniamy nazwę nowej zmiennej na s2p. Klikamy w pole wyboru przekształcenia. Poprzednio były tam tylko dwie pozycje Brak oraz Utwórz nowe przekształcenie, teraz jest trzecia pozycja Likert2R5, czyli przekształcenie, które zdefiniowaliśmy dla zmiennej s1p. Wybieramy Likert2R5, bo zmienną s2 chcemy przekodować dokładnie w ten sam sposób jak s1. Po wybraniu przekształcenia w oknie danych pojawia się nowa zmienna s2p (por. rys. 6.8).

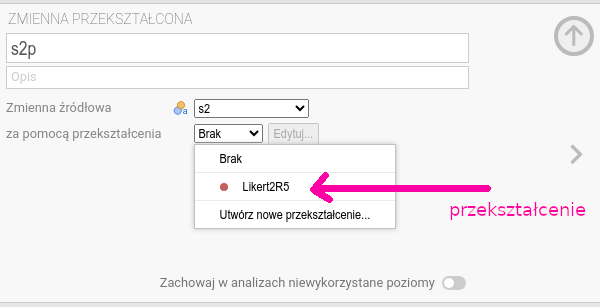
Rysunek 6.8: Przekształcenie

W podobnie łatwy sposób przekodowujemy s3 oraz zo1, zo2, zo3.

Uwaga: polecenie IF wpisujemy, używając dużych liter. Słowo $source wpisujemy tak jak jest to zademonstrowane ($Source jest błędem).

Przekodowanie pytania z możliwością wielokrotnego wyboru jest równie proste, tyle że pisania jest więcej. Zmienna wiedza_na_temat_palenia może zawierać do ośmiu następujących napisów oddzielonych średnikami: Przewlekła obturacyjna choroba płuc, Astma oskrzelowa, Alergie wziewne, Gruźlica (B), Zapalenie płuc (B), Przewlekłe zapalenie oskrzeli, Infekcje dróg oddechowych, Palenie nie powoduje chorób układu oddechowego (B).

Odpowiedzi błędne oznaczono jako (B).

W arkuszu lub oknie danych Jamovi ta zmienna wygląda jakoś tak:

...,Przewlekła obturacyjna choroba płuc,...
...,Przewlekła obturacyjna choroba płuc;Astma oskrzelowa;...
...,Astma oskrzelowa,
...,Astma oskrzelowa;Gruźlica;Przewlekłe zapalenie oskrzeli,...
...,Przewlekła obturacyjna choroba płuc;Astma oskrzelowa;...

Należy zsumować wystąpienia poprawne i wystąpienia błędne. W tym celu trzeba utworzyć tyle nowych zmiennych, ile jest wariantów odpowiedzi, czyli w naszym przykładzie osiem. Każda nowa zmienna jest przekodowywana za pomocą prostej formuły wykorzystującej funkcję CONTAINS (zawiera). Przykładowo pierwsza (nazwijmy ją wiedz1p) powinna być utworzona w oparciu o następujące przekształcenie:

CONTAINS("Przewlekła obturacyjna choroba płuc", $source)

Jak to wygląda w oknie programu Jamovi, pokazano na rysunkach 6.9 i 6.10.

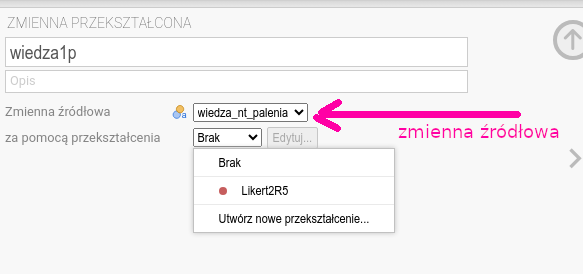
Rysunek 6.9: Przekształcenie

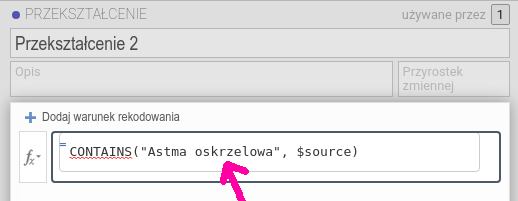
Rysunek 6.10: Przekształcenie

Funkcja CONTAINS wstawi 1, jeżeli $source zawiera frazę Przewlekła obturacyjna choroba płuc. Oczywiście następna zmienna powinna zawierać frazę Astma oskrzelowa:

CONTAINS("Astma oskrzelowa", $source)

I tak dalej aż do ostatniego wariantu odpowiedzi:

CONTAINS('Alergie wziewne', $source)
CONTAINS('Gruźlica', $source)
CONTAINS('Zapalenie płuc', $source)
CONTAINS('Przewlekłe zapalenie oskrzeli', $source)
CONTAINS('Infekcje dróg oddechowych', $source)
CONTAINS('Palenie nie powoduje chorób układu oddechowego', $source)

Każda zmienna wiedza1p…wiedza8p zawiera 1, jeżeli ankietowany wskazał dany wariant lub zero jeżeli nie wskazał.

Ostatnia sprawa to przekodowanie liczb na wartości nominalne. Przykładowo chcemy podzielić ankietowanych na klasy stażowe: mały (do pięciu lat), średni (5–15 lat), duży (16 i więcej) staż pracy.

Wartości liczbowe stażu pracy zawiera zmienna staz. Aby ją przekodować należy utworzyć nową zmienną, np. staz.klasa i zastosować przekształcenie:

IF ($source < 5, "M",
  IF ($source < 16, "S", "D"))

Poleceń IF musi być o jedno mniej niż mamy klas. Jeżeli staz jest mniejszy od 5, wstawiony zostanie napis M, jeżeli staz jest mniejszy od 16, wstawiony zostanie napis S, a w przeciwnym wypadku zostanie wstawiony napis D.

Gdyby ktoś się niepokoił, że 3 spełnia jednocześnie $source < 5 oraz $source < 16, to dodamy, że pierwszy się liczy. Przekształcenie kończy działanie po spełnieniu pierwszego warunku i nie wykonuje dalszych porównań. Dlatego liczba 3 zostanie zamieniona na M, a nie na S.

6.2.3 Wyliczenie nowych zmiennych

Przekodowanie to była w zasadzie zamiana sposobu mierzenia. Wyliczenie to utworzenie nowej zmiennej, zwykle w oparciu o jakąś formułę matematyczną. Na przykład odwrócenie pytanie s1p realizuje s1pr = 6 - s1p. Satysfakcja to suma rang z trzech pytań: satysfakcja = s1pr + s2p + s3p.

W celu wyliczenia nowych zmiennych należy wybrać Dane→Oblicz. Pojawia się okno zmiennej wyliczonej zatytułowane ZMIENNA WYLICZONA.

Pierwszy pasek zawiera nazwę zmienną (domyślnie nazwę kolumny w konwencji arkusza kalkulacyjnego, w przykładzie jest to litera H). W polu definiowania zmiennej należy wpisać stosowną formułę matematyczną. W przypadku odwracania pytania s1p będzie to:

6 - s1p

W przypadku liczenia łącznej satysfakcji (por. rys. 6.11):

SUM(s1pr, s2p, s3p)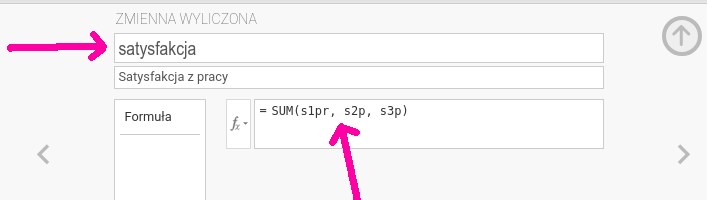

Rysunek 6.11: Obliczanie nowej zmiennej

Oczywiście wcześniej musimy utworzyć zmienną s1pr, inaczej Jamovi zgłosi błąd.

Jeżeli nie chcemy sumy, ale np. średnią, powinniśmy użyć:

MEAN(s1pr, s2p, s3p)

Inne funkcje matematyczne są dostępne po kliknięciu w pole wyboru znajdujące się po lewej stronie pola definiowania zmiennej.

Powiedzieliśmy, że miarą wiedzy nt. palenia będzie suma punktów uzyskanych za odpowiedzi prawidłowe minus suma punktów uzyskanych za odpowiedzi nieprawidłowe. Odpowiedzi prawidłowe to w1p, w2p, w3p, w6p oraz w7p. Odpowiedzi błędne to w4p, w5p, w8p. Zatem w polu definiowania zmiennej wpisujemy:

SUM(w1p, w2p, w3p, w6p, w7p) - SUM(w4p, w5p, w8p)

Dla utrwalenia utwórzmy jeszcze zmienną zo mierzącą zamiar odejścia z pracy:

SUM(zo1, zo2, zo3)

Czytelnikom pozostawiamy do samodzielnego wykonania (proste) przekształcenie zmiennej liczbowej zo na zmienną nominalną zamiarO.klasa, przyjmującą tylko dwie wartości W oraz N (co oznacza wysoki oraz niski poziom zamiaru odejścia). Przykładowo można przyjąć wartość 12 i więcej jako poziom wysoki, a mniej niż 12 jako poziom niski.

6.2.4 Analiza struktury

Wybieramy Analizy→Eksploracja→Statystyki opisowe.

W wyświetlonym oknie po lewej deklarujemy, co ma być liczone. Wynik pojawi się po prawej (por. rys. 6.12).

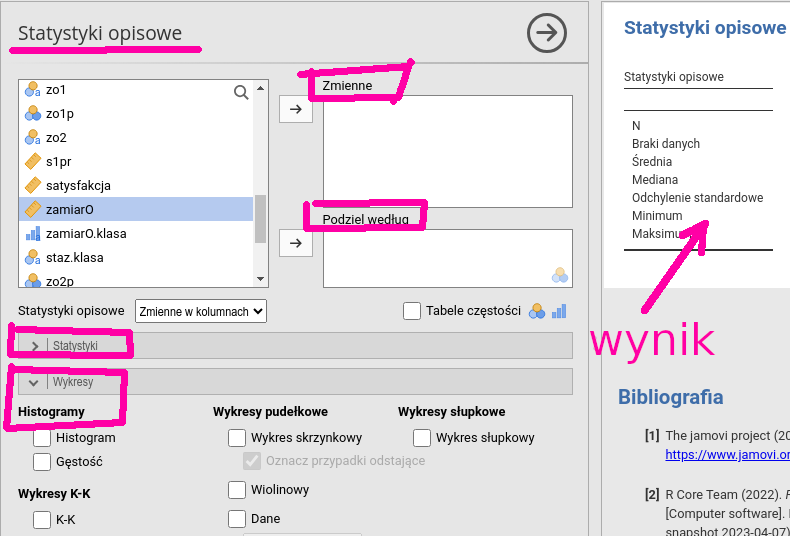
Rysunek 6.12: Statystyki opisowe

Ustawiamy kursor na zmiennej, która nas interesuje i klikamy w strzałkę górną. Jeżeli chcemy podzielić wartości zmiennej na grupy według jakiejś zmiennej nominalnej, to ustawiamy kursor na tej zmiennej nominalnej (np. plec) i klikamy strzałkę dolną.

Można analizować wiele zmiennych na raz (por. rys. 6.13). Wystarczy w tym celu ustawić kursor na zmiennej i kliknąć w odpowiednią strzałkę. Zawartość okna wynikowego zostanie automatycznie uaktualniona.

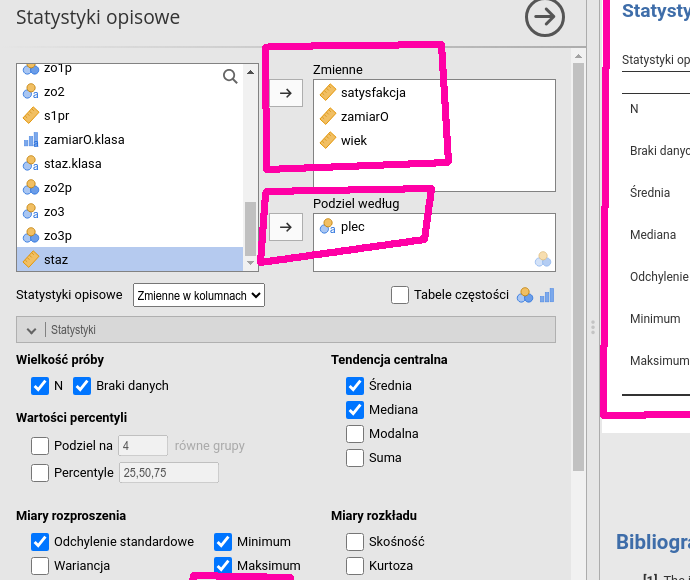
Rysunek 6.13: Statystyki opisowe

Poniżej okien wyboru zmiennych są zakładki określające precyzyjnie, co ma być obliczone oraz jakie wykresy mają zostać wyrysowane. Przykładowo domyślny wydruk nie zawiera rozstępu ćwiartkowego. Żeby go dodać do wyniku, należy w zakładce Statystyki zaznaczyć przycisk IQR.

6.2.5 Analiza zależności: zmienne nominalne

Wybieramy Analizy→Częstości→Próby niezależne.

Podobnie jak w przypadku analizy struktury jest wyświetlana lista zmiennych oraz okna i strzałki pozwalające wygodnie wybrać to, co ma być analizowane. Jest to tak proste, że wystarczy przyjrzeć się przykładowemu rysunkowi, żeby wiedzieć, jak postępować. Przykładową analizę zależności pomiędzy zmiennymi nominalnymi zamiarOklasa (zamiar odejścia) oraz staz.klasa (staż w podziale na trzy wartości) przedstawia rysunek 6.14.

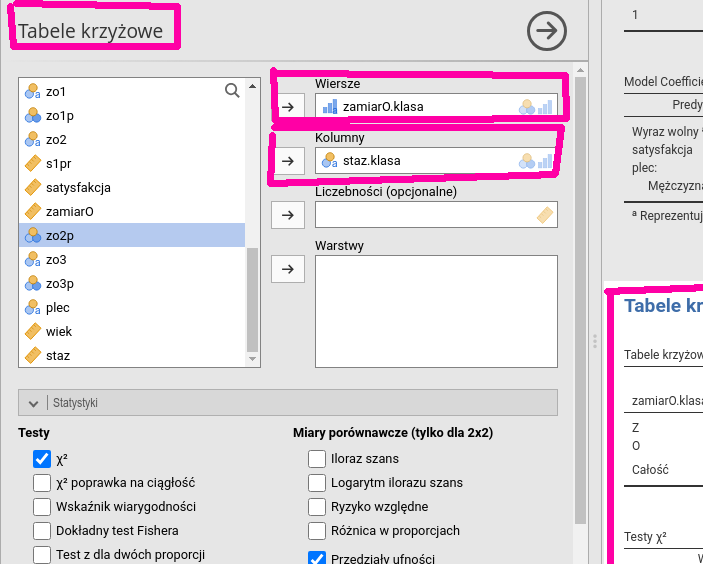
Rysunek 6.14: Tabele krzyżowe

6.2.6 Analiza zależności: zmienna liczbowa/zmienna nominalna

Jeżeli zmienna nominalna (zwana grupującą) przyjmuje dwie wartości, wybieramy Analizy→Testy t→Test t dla prób niezależnych. Zmienne zależne to zmienne, których wartości zostaną podzielone na grupy. Ustawiamy kursor kolejno na zmiennej, która nas interesuje i klikamy w strzałkę górną. Ustawiamy kursor na zmiennej grupującej (np. plec) i klikamy strzałkę dolną (por. rys. 6.15).

Zaznaczamy przyciski Test Welcha, U Manna-Whitneya (wsekcji Testy) oraz Test normalności (w sekcji Weryfikacja założeń).

Jeżeli zmienna nominalna (grupująca) przyjmuje więcej niż dwie wartości, wybieramy Analizy→ANOVA→Jednoczynnikowa ANOVA. Zmienne zależne i grupujące wybieramy w identyczny sposób jak w przypadku testu Welcha (por. rys. 6.16). Zaznaczamy przyciski Nie zakładaj równości (test Welcha) (w sekcji Wariancje) oraz Test normalności (w sekcji Weryfikacja założeń) i Tabela statystyk opisowych (w sekcji Dodatkowe statystyki).

Jeżeli wynik testu Shapiro-Wilka wskaże, że rozkład zmiennej zależnej nie jest normalny, należy wykonać test Kruskala-Wallisa, wybierając Jednoczynnikowa ANOVA Test Kruskala-Wallisa.

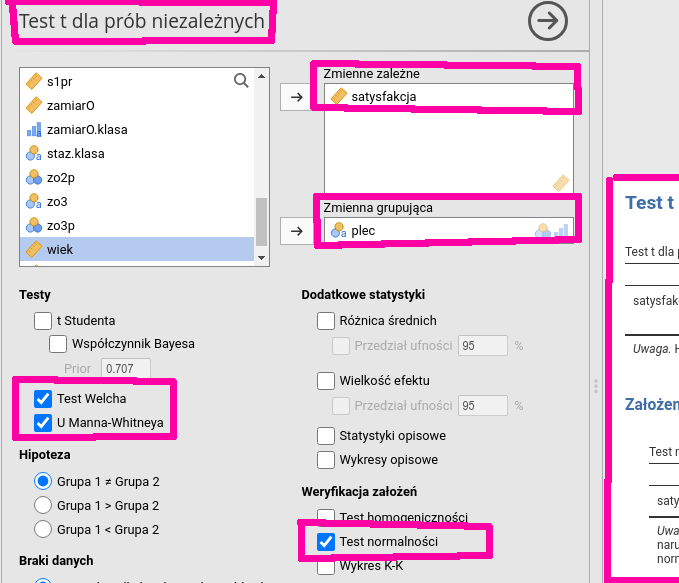
Rysunek 6.15: Test dla prób niezależnych

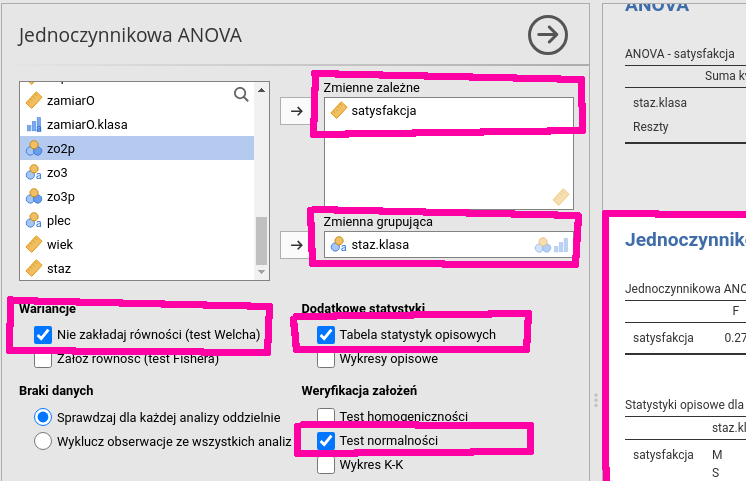
Rysunek 6.16: Jednoczynnikowa ANOVA

6.2.7 Analiza zależności: zmienna liczbowa/zmienna liczbowa lub nominalna

Wybieramy Analizy→Regresja→Regresja liniowa.

Interfejs jest podobny do poprzednio opisywanych. Wybieramy zmienną zależną (musi oczywiście być liczbowa), klikając w górną strzałkę. Zmienne niezależne mierzone w skali liczbowej wybieramy, klikając w środkową strzałkę, a zmienne niezależne mierzone w skali nominalnej – w dolną strzałkę. Wynik automatycznie pojawia się w lewym oknie (por. rys. 6.17).

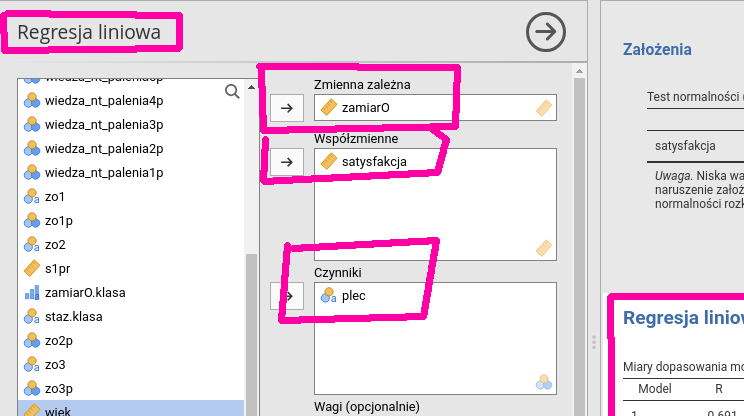
Rysunek 6.17: Regresja liniowa

6.2.8 Regresja logistyczna

Wybieramy Analizy→Regresja→Regresja logistyczna→Dwie wartości.

Interfejs jest łudząco podobny do analizy regresji. Wybieramy zmienną zależną, klikając w górną strzałkę. Zmienna ta musi być zmienną dwuwartościową.

Zmienne niezależne mierzone w skali liczbowej wybieramy, klikając w środkową strzałkę, a zmienne niezależne mierzone w skali nominalnej, klikając w dolną strzałkę.

6.2.9 Redagowanie raportu

Zwykle dobrze jest dodać jakieś dodatkowe objaśnienia do wyników obliczeń wygenerowanych przez program i Jamovi nam to umożliwia. Wybierając Edytuj, przechodzimy do prostego edytora umożliwiającego redagowanie raportu w oknie wyników, a obsługa tego menu jest tak banalnie prosta, że nie wymaga specjalnych objaśnień.